債券の利回り|FP2級Wiki
利付債の4つの利回りについて学習しましょう。複雑な式なのでなかなか暗記が難しいです。記号化して覚えるのもおすすめです。私は年利子は「利」、額面は「額」、期間は「期」とか短くしていました。
1.利付債の利回り計算
発行から償還まで保有する応募者利回り、途中購入から償還までの最終利回り、途中で売却する場合の所有期間利回り、1年間の利子のみを計算する直接利回り。この4つの計算法を紹介します。
1.応募者利回り
新規発行された債券(新発債)を購入し、償還期限まで所有した場合の利回り。最初から最後まで持っていた場合の基本形ですね。表示がクーポンとなっていますが、クーポンとは利子の事です(ここでは年利子)。
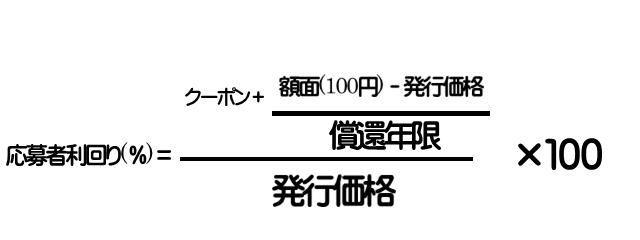
2.最終利回り
すでに発行された債券(既発債)を時価で購入し、償還期限まで所有した場合の利回り。
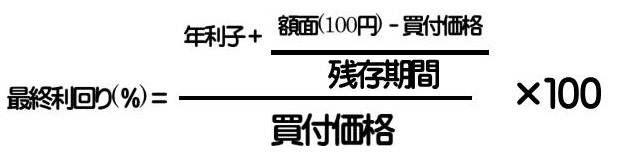
3.所有期間利回り
債券を償還期限まで所有せず、途中売却した場合の利回り。
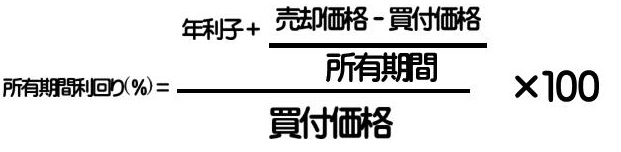
4.直接利回り
投資金額に対して1年間に得られる利子の割合を表した利回り(売却損益、償還差損益を考慮しない)。

2.イールドカーブ
イールドとは利回りの事。
債券の残存年数と利回りの関係を表す曲線の事を言う。
この曲線の表はひとつの債券の動きを示すわけではなく、同等の債券で残存年数が異なる複数の債券を1本の曲線で描いたものである。
全体の利回り水準や、短期債と長期債との利回りの関係などを読み取ることができる。
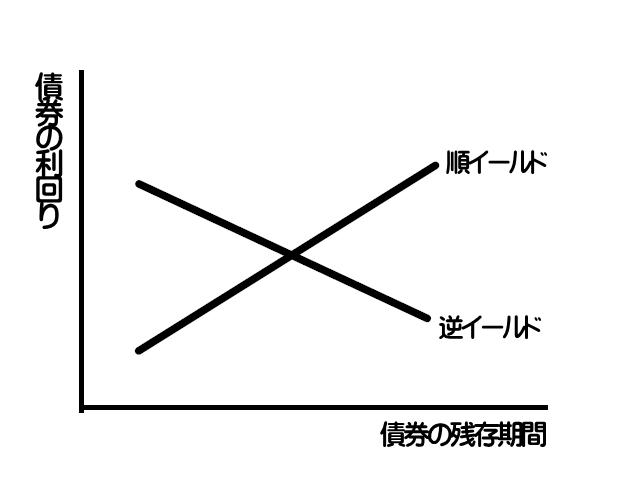
短期の債券よりも長期の債券の利回りが高い場合はイールドカーブは順イールド(右上がり)となり、
短期の債券よりも長期の債券の利回りが低いと逆イールド(右下がり)の状態になる。
一般的には長期になれば高金利になるので順イールドが普通の状態である。
短期と長期の金利差が大きくなることをスティープ化するという。
逆に差が縮まることをフラット化するという。
3.デュレーション
デュレーションには2つの意味があります。
ひとつは投資の平均回収期間(投資した分のお金を回収する平均期間)を示す尺度。
もうひとつは市場金利の変化に対する債券価格の変動性を示す尺度(金利リスク指標)です。
デュレーション(平均回収期間)が長い債券は、期間が長い分それだけいろいろなことが起きる可能性があるため、金利リスクが大きい。
クーポン(利息)が高いとデュレーションは短くなります(早く元本が回収できるから)。
つまりデュレーションが短い債券は価格変動性が低く金利リスクは小さいということになります。
※割引債には利子がないため、債券の残存期間とデュレーションは等しくなる。
外部リンク:財務省,スタディング FP講座
それでは過去問を解いてみましょう。2019年1月試験 学科 問24
表面利率が0.5%、残存期間が3年の固定利付債券を額面100円当たり102円で購入し、償還された場合の最終利回りとして、正しいものはどれか。なお、手数料、経過利子、税金等は考慮しないものとし、解答は表示単位の小数点以下第3位を四捨五入するものとする。また、「▲」はマイナスを意味するものとする。
- ▲1.47%
- ▲0.65%
- ▲0.16%
- 0.49%
.
.
.
解答
3
テキストの最終利回りの式に当てはめて計算してみましょう。 式は、(年利子+((額面-買付価格)÷残存期間))÷買付価格×100です。 1行で表すとめちゃむず!バラシて説きます。 年利0.5+(額面100-買付102)÷期間3=▲0.16 ▲0.16÷102×100=▲0.1568 よって▲0.16%です!